SpringCloud项目开源
本文共 517 字,大约阅读时间需要 1 分钟。
SpringCloud 2.x
介绍
这是一个SpringCloud 2.x项目会长久维护(SpringCloud+SpringBoot2.0)
该SpringCloud整体采用:
- Eureka(服务注册中心)
- Feign(声明式服务调用)
- Hystrix(服务熔断以及服务降级)
- Dashboard(服务监控)
- Gatway(网关)
- Sleuth+Zipkin(链路追踪)
- logback(日志)
- SpringBoot 2.x
- SpringCloud Finchley.SR1
安装教程
- 在根目录直接mvn clean install
- 首先启动RegistryApplication做服务注册中心
- 启动服务提供者ProviderApplication(数据库文件在根目录下)
- 启动服务消费者ConsumerApplication
- 启动监控中心和监控集群:DashboardApplication+DashboardClusterApplication
- 启动网关GatewayApplication
- 启动链路追踪ZipkinApplication
- 测试服务:
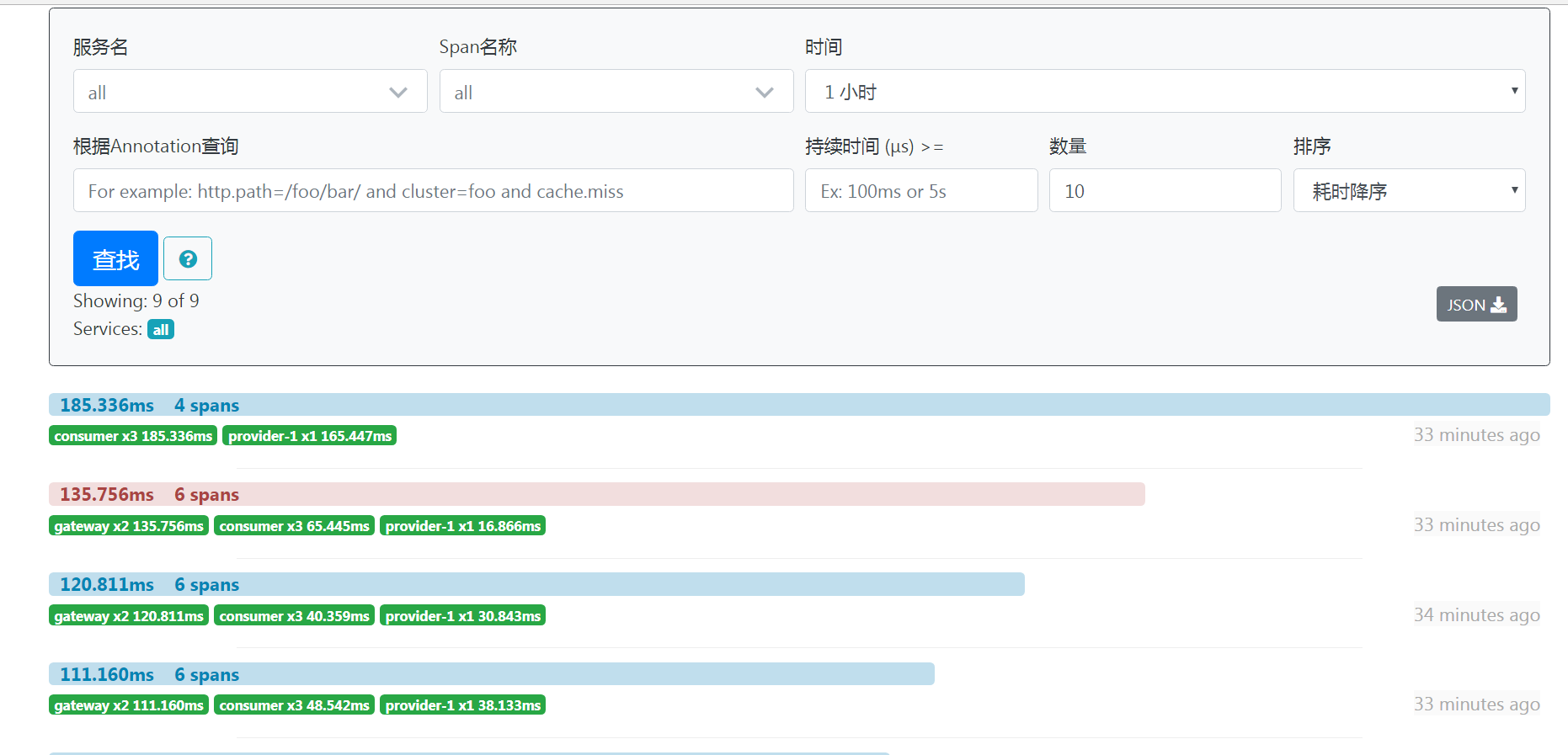
其中日志也实现了链路追踪方便线上调试: 
项目地址:
帮我star一下也行哦
转载地址:http://brmsz.baihongyu.com/
你可能感兴趣的文章
MQTT工作笔记0007---剩余长度
查看>>
MQTT工作笔记0009---订阅主题和订阅确认
查看>>
Mqtt搭建代理服务器进行通信-浅析
查看>>
MS Edge浏览器“STATUS_INVALID_IMAGE_HASH“兼容性问题
查看>>
ms sql server 2008 sp2更新异常
查看>>
MS UC 2013-0-Prepare Tool
查看>>
MSBuild 教程(2)
查看>>
msbuild发布web应用程序
查看>>
MSB与LSB
查看>>
MSCRM调用外部JS文件
查看>>
MSCRM调用外部JS文件
查看>>
MSEdgeDriver (Chromium) 不适用于版本 >= 79.0.313 (Canary)
查看>>
MsEdgeTTS开源项目使用教程
查看>>
msf
查看>>
MSSQL数据库查询优化(一)
查看>>
MSSQL数据库迁移到Oracle(二)
查看>>
MSSQL日期格式转换函数(使用CONVERT)
查看>>
MSTP多生成树协议(第二课)
查看>>
MSTP是什么?有哪些专有名词?
查看>>
Mstsc 远程桌面链接 And 网络映射
查看>>